Accueil Dictionnaire Dessin: Les bases Coques en forme Débuter un plan Détails bouchain Surf. développables Outils Mathématiques Calcul d'une surfaçes Conception: Le programme Devis de poids Courbe des Aires	Surfaces développables      La particularité d'une coque à bouchain est qu'elle doit être développable. Pour se représenter ce qu'est une forme développable, prenons une feuille de papier et cintrons la pour faire coïncider  deux de ses bords opposés. Nous obtenons un cylindre. Avec la même feuille, nous prenons un coin pour le faire coïncider avec un coté nous fabriquons un cône.      En faisant ce petit exercice nous avons construit des formes constituées de lignes courbes, et de lignes droites. Ce sont des formes développables. Les lignes droites  se nomment les génératrices. Pour dessiner une coque à bouchain, nous  nous servirons de portions de cône, et de portions de cylindre. Dans un cylindre toutes les génératrices sont parallèles. Dans un cône toutes les génératrices se rejoignent en un même point nommé pôle.       Lorsque nous avons confectionné notre cylindre, nous nous sommes appliqués pour que la section soit bien ronde. Mais nous pouvons déformer notre feuille, sans chercher à ce que les deux bords se rejoignent, lui imposer une forme s'approchant du S.
	Cette surface sera toujours dèveloppable les génératrices seront parallèles par contre le bord de la feuille suivra une ligne indéterminée mais régulière. Cette ligne s'appelle la directrice. Lorsque nous avons confectionné notre cylindre, la directrice était parfaitement définie, c'était un cercle. Pour faire le cornet de frite nous avons du rabattre à l'intérieur du cône l'excédant de papier, pour obtenir à une extrémité un rond, et à l'autre une pointe. Donc pour un cône l'une de ses extrémité est un point, l'autre est un cercle.  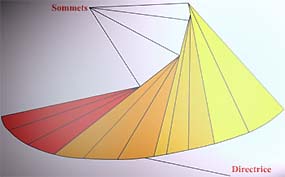En combinant ces particularités nous pourrons dessiner d'autres formes développables variées. Exemple: Les cônes glissants. Chaque portion de cône glisse sur la génératrice du cône précédent. Nous pourrions avoir une infinité de cônes accolés, glissant sur la génératrice du cône précédent. Nous pouvons également associer des cônes et des cylindres. Il suffit pour cela qu'ils aient une génératrice commune.